IOSG Weekly Brief ｜零知识证明 - FPGA vs GPU

零知识证明技术应用越来越广，隐私证明，计算证明，共识证明等等。在寻找更多更好的应用场景的同时，很多人逐步发现零知识证明证明性能是个瓶颈。Trapdoor Tech 团队从 2019 年开始深入研究零知识证明技术，并一直探索高效的零知识证明加速方案。GPU 或者 FPGA 是目前市面上比较常见的加速平台。本文从 MSM 的计算入手，分析 FPGA 和 GPU加速零知识证明计算的优缺点。

TL;DR

ZKP是拥有未来广泛前景的技术。越来越多的应用开始采用零知识证明技术。但ZKP算法比较多，各种项目使用不同的ZKP算法。同时，ZKP证明的计算性能比较差。本文详细分析了MSM算法，椭圆曲线点加算法，蒙哥马利乘法算法等等，并对比了GPU和FPGA在BLS12_381曲线点加的性能差别。总的来说，在ZKP证明计算方面，短期GPU优势比较明显，Throughput高，性价比高，具有可编程性等等。FPGA相对来说，功耗有一定的优势。长期看，有可能出现适合ZKP计算的FPGA芯片，也可能为ZKP定制的ASIC芯片。

ZKP 算法复杂

ZKP是个零知识证明技术的统称（Zero Knowledge Proof）。主要由两种分类：zk-SNARK以及zk-STARK。zk-SNARK目前常见的算法是Groth16，PLONK，PLOOKUP，Marlin和Halo/Halo2。zk-SNARK算法的迭代主要是沿着两条方向：1/是否需要trusted setup 2/电路结构的性能。zk-STARK算法的优势是毋需trusted setup，但是验证计算量是对数线性的。

就zk-SNARK/zk-STARK算法的应用来看，不同项目使用的零知识证明算法相对分散。zk-SNARK算法应用中，因为PLONK/Halo2算法是universal（无需trusted setup），应用可能越来越多。

PLONK 证明计算量

以PLONK算法为例，剖析一下PLONK证明的计算量。

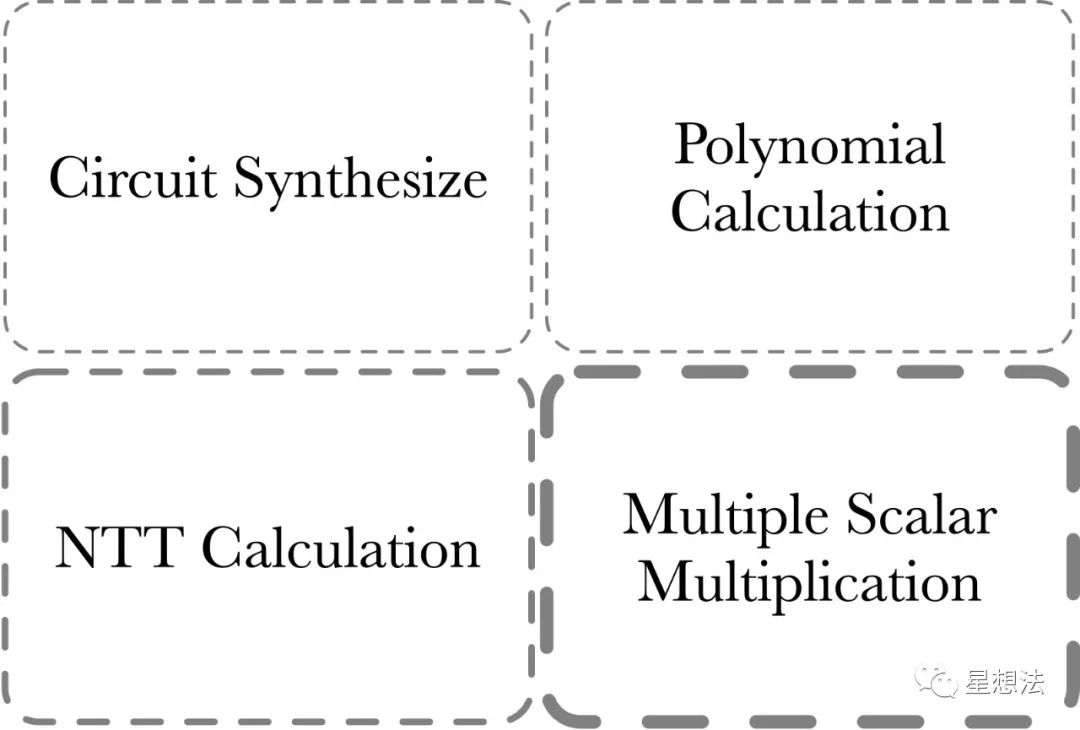
PLONK证明部分的计算量由四部分组成：

1/ MSM - Multiple Scalar Multiplication。MSM经常用来计算多项式承诺。

2/ NTT计算 - 多项式在点值和系数表示之间变换。

3/ Polynomial计算 - 多项式加减乘除。多项式求值（Evaluation）等等。

4/ Circuit Synthesize - 电路综合。这部分的计算和电路的规模/复杂度有关。

Circuit Synthesize部分的计算量一般来说判断和循环逻辑比较多，并行度比较低，更适合CPU计算。通常来讲，零知识证明加速一般指的是前三部分的计算加速。其中，MSM的计算量相对来说最大，NTT次之。

What's MSM

MSM（Multiple Scalar Multiplication）指的是给定一系列的椭圆曲线上的点和标量，计算出这些点加的结果对应的点。

比如说，给定一个椭圆曲线上的一系列的点：

Given a fixed set of Elliptic curve points from one specified curve:

[G_1, G_2, G_3, ..., G_n]

以及随机的系数：

and a randomly sampled finite field elements from specified scalar field:

[s_1, s_2, s_3, ..., s_n]

MSM is the calculation to get the Elliptic curve point Q:

Q = \sum_{i=1}^{n}s_i*G_i

行业普遍采用Pippenger算法对MSM计算进行优化。深入看看Pippenger算法的过程的示意图：

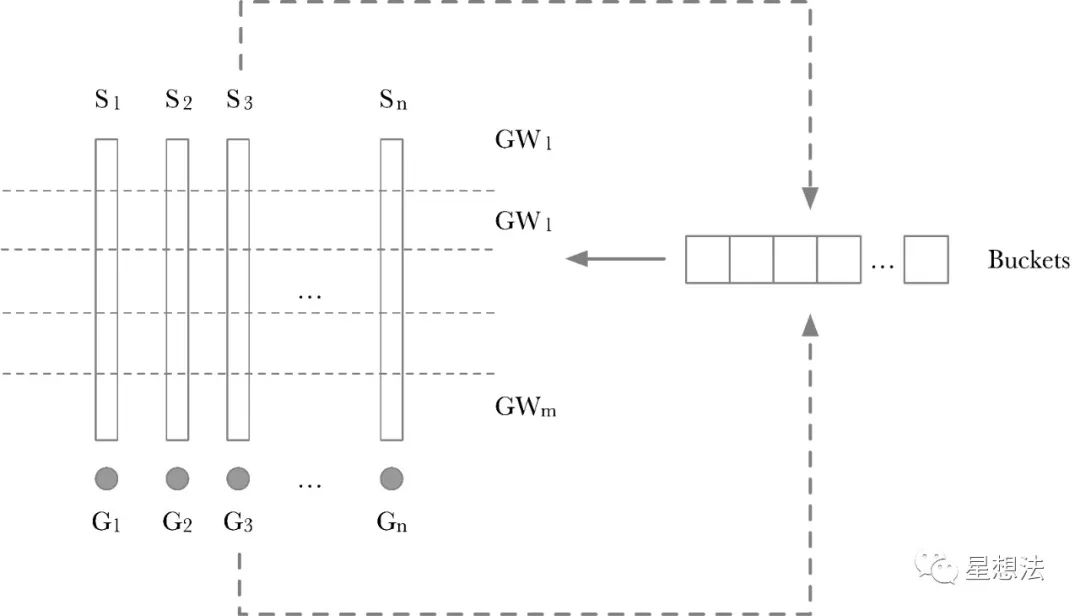
Pippenger算法的计算过程分成两步：

1/ Scalar切分为Windows。如果Scalar是256bits，并且一个Window是8bits，则所有的Scalar切分为256/8=32个Window。每一层的Window，采用一个“Buckets”临时存放中间结果。GW_x就是一层上的累加结果的点。计算GW_x也比较简单，依次遍历一层中的每个Scalar，根据Scalar这层的值作为Index，将对应的 G_x加到相应的Buckets的位上。其实原理也比较简单，如果两个点加的系数相同，则先将两个点相加后再做一次Scalar加，而不需要两个点做两次Scalar加后再累加。

2/ 每个Window计算出来的点，再通过double-add的方式进行累加，从而得到最后的结果。

Pippenger算法也有很多变形优化算法。不管怎么说，MSM算法的底层计算就是椭圆曲线上的点加。不同的优化算法，对应不同的点加个数。

椭圆曲线点加（Point Add）

你可以从这个网站看看具有“short Weierstrass”形式的椭圆曲线上点加的各种算法。

http://www.hyperelliptic.org/EFD/g1p/auto-shortw-jacobian-0.html#addition-madd-2007-bl

假设两个点的Projective坐标分别为（x1, y1, z1) 和 （x2, y2, z2) ，则通过如下的计算公式可以计算出点加的结果(x3, y3, z3)。

详细给出计算过程的原因是想表明整个计算过程绝大部分是整数运算。整数的位宽取决于椭圆曲线的参数。给出一些常见的椭圆曲线的位宽：

• BN256 - 256bits
• BLS12_381 - 381bits
• BLS12_377 - 377bits
• 特别注意的是，这些整数运算是在模域上的运算。模加/模减相对来说简单，重点看看模乘的原理和实现。

模乘（Modular Muliplication）

给定模域上的两个值：x和y。模乘计算指的是 x*y mod p。注意这些整数的位宽是椭圆曲线的位宽。模乘的经典算法是蒙哥马利乘法（MontgomeryMuliplication)。在进行蒙哥马利乘法之前，被乘数需要转化为蒙哥马利表示：

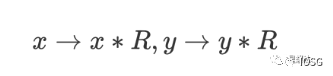
蒙哥马利乘法计算公式如下：

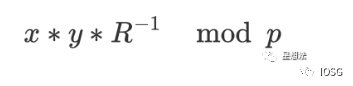
蒙哥马利乘法实现算法又有很多：CIOS (Coarsely Integrated Operand Scanning)，FIOS（Finely Integrated Operand Scanning），以及 FIPS（Finely Integrated Product Scanning）等等。本文不深入介绍各种算法实现的细节，感兴趣的读者可以自行研究。

为了对比FPGA以及GPU的本身的性能差别，选择最基本的算法实现方法：

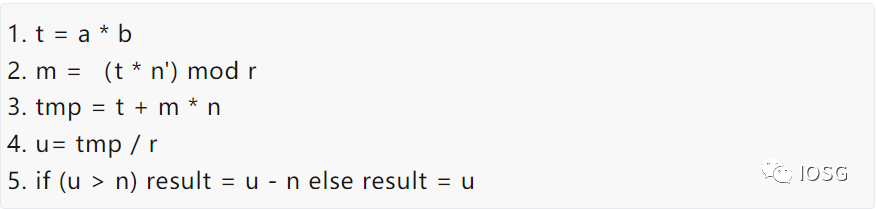
简单的说，模乘算法可以进一步分成两种计算：大数乘法和大数加法。理解了MSM的计算逻辑的基础上，可以选择模乘的性能（Throughput）来对比FPGA和GPU的性能。

观察和思考

在这样的FPGA设计下，可以估算出整个VU9P能提供的在BLS12_381椭圆曲线点加Throughput。一个点加（add_mix方式）大约需要12个模乘。FPGA的系统时钟为450M。

在同样的模乘/模加算法下，采用同样的点加算法，Nvidia 3090的点加Troughput（考虑到数据传输因素）超过500M/s。当然，整个计算涉及到多种算法，可能存在某些算法适合FPGA，有些算法适合GPU。采用一样的算法对比的原因，想对比FPGA和GPU的核心计算能力。

基于上述的结果，总结一下GPU和FPGA在ZKP证明性能方面的比较：

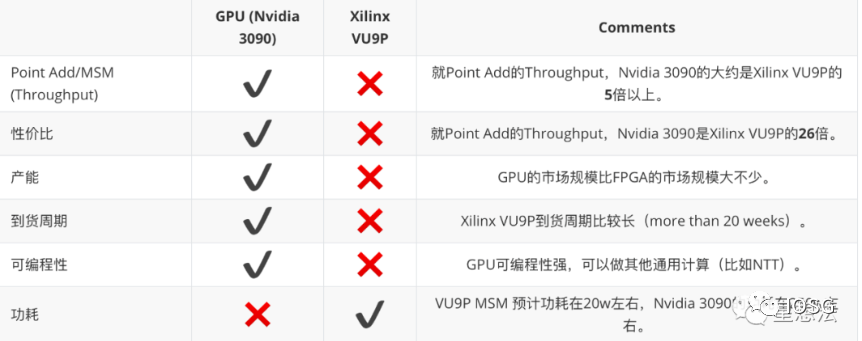
总结

越来越多的应用开始采用零知识证明技术。但ZKP算法比较多，各种项目使用不同的ZKP算法。从我们的实践工程经验来看，FPGA是个选项，但是目前GPU是个性价比高选项。FPGA偏好确定性计算，有latency以及功耗的优势。GPU可编程性高，有相对成熟的高性能计算的框架，开发迭代周期短，偏好需要throughput场景。